

2.0- LA LOGIQUE COMBINATOIRE Circuits de logique combinatoire - élaboration de la table de vérité.
2.1 - Définition: On obtient en sortie le résultat de la combinaison de plusieurs entrées. Le résultat est instantanné. Cette fonction est vue au moyen de la table de vérité.
2.2 - Les porte logiques.
| Porte OUI |  |  |
La sortie reproduit le niveau d'entrée. |

| Porte NON |  |  |
La sortie reproduit le niveau inverse d'entrée. |
| Porte ET (AND) |  |
Les portes ET possédent plusieurs entrées: e1, e2, e3, e... La sortie est au niveau 1 si toutes les entrées sont également au niveau 1 Une seule entrée au niveau 0 suffit pour que la sortie soit à 0 |
| Porte ET-NON (NAND) |  |
Les portes ET-NON possédent plusieurs entrées: e1, e2, e3, e... La sortie est au niveau 0 si toutes les entrées sont au niveau 1 Une seule entrée au niveau 0 suffit pour que la sortie soit à 1 |
| Porte OU (OR) |  |
Les portes OU possédent plusieurs entrées: e1, e2, e3, e... La sortie est au niveau 1 si une des entrées est au niveau 1 Une seule entrée au niveau 1 suffit pour que la sortie soit à 1 |
| Porte OU-NON (NOR ) | 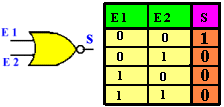 |
Les portes OU-NON possédent plusieurs entrées: e1, e2, e3, e... La sortie est au niveau 1 si aucune des entrées est au niveau 0 Une seule entrée au niveau 1 suffit pour que la sortie soit à 0 |
| Porte EXOR |  |
Les portes OU-EXCLUSIF (EXOR) possédent deux entrées: e1, e2. La sortie est au niveau 1 si une des entrées est au niveau 1 et pas les deux. S = (E1 ou E2) et pas (E1 et E2) La sortie est au niveau 1 quand les deux entrées sont contraires. |
| Porte EXNOR |  |
Les portes NON-OU-EXCLUSIF (EXNOE) possédent deux entrées: e1, e2. La sortie est au niveau 0 si une des entrées est au niveau 1 et pas les deux. S = (E1 ou E2) et pas (E1 et E2) La sortie est au niveau 0 quand les deux entrées sont contraires. |